Death to... test what you think you know

[Jay Barracato]

I had been turning over the possible effects of stacking a fully cut graphic eq on top of a crossover in my mind, I was was coming up against 2 apparently conflicting interpretations as to whether this would make a difference so I decided to measure it.

By "death to..." I mean the practice of cutting frequency bands on an eq that are then further cut by a crossover.

Best professional practices say "Don't do it" but I was wondering if I could determine why.

What I think I know:
1. The frequency range over which an Geq filter makes a change in phase basically matches the same range in which it makes a magnitude change.
2. Adjacent frequency ranges on a Geq overlap so they also create summed changes in response in both magnitude and phase.
3. Depending on the type and slope, crossover filters make changes in magnitude and phase well beyond their "label" frequency.
4. Stacking filters, i.e. Geq followed by crossover, should give a response in phase and magnitude based on the summation of the filters which includes their relative sizes.

What I am not as sure of that I would like to be:
1. Do multiple filters create a change in phase response BEYOND the region where they make a magnitude change?

The two possible interpretations that I came up with:

1. Cutting all the frequency bands by 12 db will make an audible difference because the phase is affected by all those cuts.
2. Cutting all the frequency bands by 12 db will not make an audible difference because even though the phase is affected, the magnitude is so low that it doesn't matter.

Now the kicker that confused things:

Would having multiple cuts on a Geq below the crossover point affect the phase enough that it would mess up the phase AT the crossover point?

So today I was not in the position to measure the acoustic crossover of a sub/top combination, I was in the position to measure the electronic crossover of a sub top combination, both with and without the "death to..." Geq.

The null hypothesis: There is no difference in the phase response at the crossover between the "No Geq" test and the "Death to..." test.

The alternative hypothesis: There is a difference in the phase response at the crossover between the "No Geq" test and the "Death to..." test.

The experimental setup: Two channel measurement of phase and magnitude using SMAART of a pink noise signal passed through a KT DN360 Geq and a Sabine navigator DSP.

Controls: The KT DN360 and the Sabine Navigator were measured as flat in phase and magnitude both individually and in series with no filters in place prior to setting up the crossovers.

The crossover were set up using LR filters with both 12 db/octave and 48 db/octave slopes. The results were measured both with and without the "Death to.." Geq filters in place.

The results:

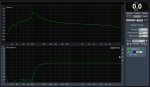
LR 12 db/octave with no geq (with polarity flip to match the phases)


LR 12d/octave with "Death to..." cuts above and below the crossover


The phase traces no longer lie on top each other above and below the crossover, and the summed magnitude response at the crossover is far below the trace with no eq

LR 48 db/octave with no Geq


Once again the phase traces lie on top of each other nicely over the entire crossover range.


LR 48 db/octave with "death to..." Geq added



This is the one I really wondered about because the magnitude from the steep slope is already so great that the extremes of the phase and magnitude wasn't even measured (note the coherence in the region away from the crossover). However; once again, there is a fairly large change in the timing of the phase that has been introduced.

So my conclusion is that the "Death to... " Geq technique does introduce significant changes in the behavior of the electronic crossover without any added benefit. (The null hypothesis is rejected and the alternative hypothesis accepted). The phase response of the 48 db/octave crossover with no eq is better than the phase response of the 12 db/octave crossover with the added 12 db cuts on the Geq.

Entering the realm of speculation, I would surmise that these negative effects the Geq has on the electronic crossover would be audible in the acoustic crossover.

 

[TJ Cornish]

Re: Death to... test what you think you know

Nice application of the scientific method! What, are you a science teacher or something?

It's very cool to see the evidence in your graphs, and not a far leap to your hypothesis of audible effects.

Thanks for taking the time.

 

[Art Welter]

Re: Death to... test what you think you know

By "death to..." I mean the practice of cutting frequency bands on an eq that are then further cut by a crossover.

LR 12d/octave with "Death to..." cuts above and below the crossover
The phase traces no longer lie on top each other above and below the crossover, and the summed magnitude response at the crossover is far below the trace with no eq

Would having multiple cuts on a Geq below the crossover point affect the phase enough that it would mess up the phase AT the crossover point?

So my conclusion is that the "Death to... " Geq technique does introduce significant changes in the behavior of the electronic crossover without any added benefit.
The phase response of the 48 db/octave crossover with no eq is better than the phase response of the 12 db/octave crossover with the added 12 db cuts on the Geq.

Jay,

I'm not sure where you are going with your conclusion.

Years ago there was a "death to 100" thread about killing everything below 100 Hz on monitor EQ, which on some EQ types also happens to kill frequencies well above 100 Hz.

If one wants to combine a LF signal with the HF signal (in which case phase response in the crossover region is important), the only reason why you would kill the LF on an EQ would be if the sub output was set way too hot and you had no access to the crossover, in which case you are stuck with the lesser of two evils, kill it on the mains EQ, or every channel.

If your goal is removing as much LF from a signal, stacking filters will aid that goal, and the LF phase response of a signal that is attenuated 24 or more dB is of no consequence.

Art

 

[Silas Pradetto]

Re: Death to... test what you think you know

Jay,

I'm not sure where you are going with your conclusion.

Years ago there was a "death to 100" thread about killing everything below 100 Hz on monitor EQ, which on some EQ types also happens to kill frequencies well above 100 Hz.

If one wants to combine a LF signal with the HF signal (in which case phase response in the crossover region is important), the only reason why you would kill the LF on an EQ would be if the sub output was set way too hot and you had no access to the crossover, in which case you are stuck with the lesser of two evils, kill it on the mains EQ, or every channel.

If your goal is removing as much LF from a signal, stacking filters will aid that goal, and the LF phase response of a signal that is attenuated 24 or more dB is of no consequence.

Art

The 48dB/octave slope graph shows nearly 180 degrees of phase difference dead on the 100Hz electrical crossover, meaning your subs and tops will be quite out of phase if you apply this EQ technique.

Of course you could measure with Smaart or similar and compensate for this, but why start with a mess and fix it?

If you're not crossing into another passband and simply highpassing, such as for monitors, this technique should not matter as it just rolls off the lows and the phase doesn't matter.

 

[Matt Lillie]

Re: Death to... test what you think you know

Jay,

I'm not sure where you are going with your conclusion.

Years ago there was a "death to 100" thread about killing everything below 100 Hz on monitor EQ, which on some EQ types also happens to kill frequencies well above 100 Hz.

If one wants to combine a LF signal with the HF signal (in which case phase response in the crossover region is important), the only reason why you would kill the LF on an EQ would be if the sub output was set way too hot and you had no access to the crossover, in which case you are stuck with the lesser of two evils, kill it on the mains EQ, or every channel.

If your goal is removing as much LF from a signal, stacking filters will aid that goal, and the LF phase response of a signal that is attenuated 24 or more dB is of no consequence.

Art

Agreed, I'm not sure why anyone in their right mind would use a setup like the test. If you're trying to get rid of the stuff under 100, why would you use a sub in the first place? Just shut the sub amp off and call it a day?

 

[Silas Pradetto]

Re: Death to... test what you think you know

Agreed, I'm not sure why anyone in their right mind would use a setup like the test. If you're trying to get rid of the stuff under 100, why would you use a sub in the first place? Just shut the sub amp off and call it a day?

Matt, as extensively discussed in other threads on this forum, people do it all the time, thinking they are 'helping' the crossover or something.

 

[Jay Barracato]

Matt, as extensively discussed in other threads on this forum, people do it all the time, thinking they are 'helping' the crossover or something.

My experience touring PACs, small clubs, listening rooms, coffeehouses, and small festivals (I.e. exactly JV level providers) was that I encountered this on about 1 in 5 systems.

The way it is most often put into use is to have the subs on an aux with its own crossover ( often built into a powered sub) and then have all the of bands on the main geq dumped.

Also it was pretty clear why it is not always the best idea to use the highest possible slope. Adding the effect on the phase of the geq to the 48 db/octave crossover added 30 degrees of rotation all the way through the typical MF/HF region.

So instead of telling people not to do it, I set out to create the visual evidence of why you shouldn't do it.

 

[Matt Lillie]

Re: Death to... test what you think you know

My experience touring PACs, small clubs, listening rooms, coffeehouses, and small festivals (I.e. exactly JV level providers) was that I encountered this on about 1 in 5 systems.

The way it is most often put into use is to have the subs on an aux with its own crossover ( often built into a powered sub) and then have all the of bands on the main geq dumped.

Also it was pretty clear why it is not always the best idea to use the highest possible slope. Adding the effect on the phase of the geq to the 48 db/octave crossover added 30 degrees of rotation all the way through the typical MF/HF region.

So instead of telling people not to do it, I set out to create the visual evidence of why you shouldn't do it.

Is there a high pass involved, or do they use the GEQ instead? I guess I can see it if there's no high pass elsewhere, in a pinch or whatever. I've dumped all of that stuff for wedges when there is no high pass other than a fixed 40. Counter productive if there's already a high pass, which I see now is your point.

 

[John Roberts]

Re: Death to... test what you think you know

In the interest of completeness it may be worth inspecting how "most" GEQ are designed. They first create individual bandpass filters for each GEQ center frequency then add or subtract that BP signal to the dry path to create boost or cut. These are pretty much a blunt instrument, a dull knife so to speak, with different topology/design philosophy variations. How adjacent bands combine and interact with each other will vary with different circuit topologies and different design trade-offs. (insert my tired Q definition rant here).

A smart digital GEQ could be taught to interpret adjacent "death to" slider settings differently, but conventional GEQs will give conventionally poor combined results. Adding deep GEQ cut near a critical crossover pole is asking for trouble as crossovers are not just about amplitude but phase response in the critical transition region.

JR

 

[Jay Barracato]

Re: Death to... test what you think you know

Here is my "death below 100" curve with NO dsp, like it may be applied to a monitor with no other DSP.


You can see how the filters add to create cuts that are larger than the 12 db applied, and that the combined effect in magnitude goes up to 300 hz, and is probably audible up to close to 200 hz. On the other hand, the effect on the phase goes up to 2000 hz, and is probably audible from 100-500 hz.

 

[Jon Waller]

Re: Death to... test what you think you know

It appears what you are really doing here is applying a 'death above 100Hz' curve to the Geq, measuring the LF crossover output, then applying a different 'death below 100Hz' curve to the Geq, then measuring the HF crossover output. This is not so obvious in your written explanation. It should be obvious that this is bad audio engineering and the matched phase response and complementary amplitude response of LR filters would be corrupted.

 

[Jay Barracato]

Re: Death to... test what you think you know

Jon,

I am not sure what you are saying. The graph I just posted is just an eq, like it would be wired in a monitor system with no other dap, just as I labeled the graph.

The first graphs are a geq then a dsp in series, just how they would be deployed. Yes there are two different bands pasted together on the same graph so you can see how they interact. You can also compare with the graph that shows the identical patching and bands, but with the Geq set flat. The only different in those two sets of measurements is where the faders on the Geq is set.

I am perfectly aware that this is bad practice. It is a bad practice I encounter all the time when working as a band engineer on other peoples systems. Since the bad practice is so common, I was attempting to show why it is a bad practice. No where have I said this is something I do or encourage others to do.

 

[Jon Waller]

Re: Death to... test what you think you know

The only different in those two sets of measurements is where the faders on the Geq is set.

Yes, but since you did not explicitly say that in your initial post, I was confused until I looked closely for a second time at the phase curve on your second set of plots, with the Geq on.

Obviously, you got it or you would not have gone to all the trouble to post this. That part of my comment was more directed at the rest of the viewers.

Actually, when I first clicked on the title of this thread, this is what I was thinking it was about!
Steel Panther - Death To All But Metal (Explicit) - YouTube

:blush:

 

[Art Welter]

Re: Death to... test what you think you know

My experience touring PACs, small clubs, listening rooms, coffeehouses, and small festivals (I.e. exactly JV level providers) was that I encountered this on about 1 in 5 system.

Jay,

What do the 20% of JV level providers you encounter who pull down everything below 100 Hz on the main EQ while using subs offer as an explanation for the idiotic practice?

 

[Tim McCulloch]

Re: Death to... test what you think you know

Jay,

What do the 20% of JV level providers you encounter who pull down everything below 100 Hz on the main EQ while using subs offer as an explanation for the idiotic practice?

You get 'em at "higher" levels, too. I've been kicking around a blog post about an encounter from a year or so ago. It involved this practice of using GEQs in the manner Jay is describing, and what things sound like when the BE is blindly loyal to his own ego.

 

[Scott Helmke]

Re: Death to... test what you think you know

One other aspect of GEQ design is that usually the sliders all have a center tap that effectively shorts out that filter, which means that it won't contribute any noise while in the center detent.

 

[Jay Barracato]

Jay,

What do the 20% of JV level providers you encounter who pull down everything below 100 Hz on the main EQ while using subs offer as an explanation for the idiotic practice?

Art,

For the most part they have no explanation. I think they are operating under the combined ideas that if they have a control that control needs to be used, and they have set the sound by ear but have also gotten used to the sound they set. The idea of phase is not a practical reality to these folks. I think part of the reason the idea of aux fed subs got so big so fast on small systems is because many operators used it as a way around setting up a sub/main crossover.

It is not uncommon to see "do not touch the eq's" signs in these places and as a BE knowing more then your host does not mean you can do what you want with their setup. Sometimes anything other than changing levels involves extensive negotiation. Their have been a number of times with bluegrass bands, I have made a system that vocally sounded like it had a blanket over the speakers come alive by simply discreetly hitting bypass on graphics and comps slapped across the main mix and just having decent gain structure through the board.

So I guess the fundamental reason they would have to give is "someone showed me that way when I didn't understand it, and since I still don't understand, I still do it that way."

 

[Jay Barracato]

Re: Death to... test what you think you know




One such system I encountered. The top photo shows 15 band Geqs in series with compressors inserted on channels. The second photo shows the house Geq on top and monitors on the bottom. Rather than being zeroed, there were similar cuts on the board for all the channels as well.

This is reality. You have 1 hour to get everything out of the van, set up on stage, and checked before the show starts. All the channels are preset, and apparently from the grunge around the knobs never change, for a 5 piece rock band. You are being helped by the third string house engineer, because the head guy didn't think it was important to be there when the band was bringing their own tech. The third string house tech doesn't seem to know anything about how the system is configured except what mics plug into the snake where. He is also not sure you should change anything because the head tech really likes how the channel is set for a strat through a twin and shouldn't that be ok for your mandolin through a LDC.

So where do you start?

(This is an extreme case, but this is a fairly well known room on the east coast circuit in the under 300 capacity that books original music nightly.)

 

[Silas Pradetto]

Re: Death to... test what you think you know

View attachment 7426
View attachment 7427

One such system I encountered. The top photo shows 15 band Geqs in series with compressors inserted on channels. The second photo shows the house Geq on top and monitors on the bottom. Rather than being zeroed, there were similar cuts on the board for all the channels as well.

This is reality. You have 1 hour to get everything out of the van, set up on stage, and checked before the show starts. All the channels are preset, and apparently from the grunge around the knobs never change, for a 5 piece rock band. You are being helped by the third string house engineer, because the head guy didn't think it was important to be there when the band was bringing their own tech. The third string house tech doesn't seem to know anything about how the system is configured except what mics plug into the snake where. He is also not sure you should change anything because the head tech really likes how the channel is set for a strat through a twin and shouldn't that be ok for your mandolin through a LDC.

So where do you start?

(This is an extreme case, but this is a fairly well known room on the east coast circuit in the under 300 capacity that books original music nightly.)

For some reason, you don't actually have to know anything to be a sound guy.

 

[Robert Patch]

Re: Death to... test what you think you know

For some reason, you don't actually have to know anything to be a sound guy.

Whew! That takes off a lot of pressure.