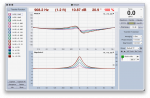
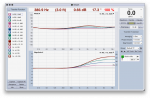
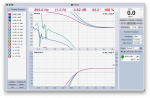
Can we discuss the theory and application?
I am really a minimalist in my approach to system eq. I really liked Jamie Anderson's suggestion of using fairly broad filters to adjust general trends rather than using a bunch for each little detail you measured.
This got me thinking about the effect of each filter on the phase response and the possibility of using out of band filters to adjust phase within the band or at a crossover.
Is this idea on track? Any hints for real world practice? Any papers to sit back and digest?
I am really a minimalist in my approach to system eq. I really liked Jamie Anderson's suggestion of using fairly broad filters to adjust general trends rather than using a bunch for each little detail you measured.
This got me thinking about the effect of each filter on the phase response and the possibility of using out of band filters to adjust phase within the band or at a crossover.
Is this idea on track? Any hints for real world practice? Any papers to sit back and digest?