Any good info on the pros/cons of FIR filters. Wanting a basic understanding of FIR and just starting to do research. Thanks!
FIR filters
- Thread starter Sean Thomas
- Start date
Re: FIR filters
How much do you want to know, and how's your math?
http://music.tutsplus.com/tutorials/filters-and-you-fir-filters--audio-23400 a good basic intro to FIR filters in audio. The same source on IIR filters http://music.tutsplus.com/tutorials/filters-and-you-iir-filters--audio-23061
http://www.iowahills.com/A8FirIirDifferences.html
http://www.dspguru.com/dsp/faqs/fir/basics
http://www.allaboutcircuits.com/technical-articles/design-of-fir-filters/
The use of filters in signal processing goes far beyond audio applications. You'll find a lot of reading.
How much do you want to know, and how's your math?
http://music.tutsplus.com/tutorials/filters-and-you-fir-filters--audio-23400 a good basic intro to FIR filters in audio. The same source on IIR filters http://music.tutsplus.com/tutorials/filters-and-you-iir-filters--audio-23061
http://www.iowahills.com/A8FirIirDifferences.html
http://www.dspguru.com/dsp/faqs/fir/basics
http://www.allaboutcircuits.com/technical-articles/design-of-fir-filters/
The use of filters in signal processing goes far beyond audio applications. You'll find a lot of reading.
Re: FIR filters
My math is not good enough to understand what I've been reading. Did about 2 hrs of research and really never found a laymen explanation of FIR filters.
I am trying to relate the FIR concept to X-over filters like LR, Butterworth, or a way of applying eq like a parametric, etc., but I don't think it's the same. What is the purpose of FIR and why is it better? Can anyone explain in basic terms?
I know a lot of speaker manufacturers update their DSP's to eventually have FIR filters and it is supposed to be WAY better. Just trying to understand that concept and why it's better. And, if better, why aren't all DSP's, powered speakers using FIR? (cost/programming time?)
Thanks!
My math is not good enough to understand what I've been reading. Did about 2 hrs of research and really never found a laymen explanation of FIR filters.
I am trying to relate the FIR concept to X-over filters like LR, Butterworth, or a way of applying eq like a parametric, etc., but I don't think it's the same. What is the purpose of FIR and why is it better? Can anyone explain in basic terms?
I know a lot of speaker manufacturers update their DSP's to eventually have FIR filters and it is supposed to be WAY better. Just trying to understand that concept and why it's better. And, if better, why aren't all DSP's, powered speakers using FIR? (cost/programming time?)
Thanks!
Re: FIR filters
Sometimes people try to fix things with the wrong tool.
Here is an analogy I like to use.
What if we made a tire that has 12 sides. Then we can use a fancy computer controlled suspension system to even out the ride. Yes it would have its drawbacks, but at least we could sell it as having "more control" (which of course it needs to begin to work properly)
WELL MAYBE----if the tire was made ROUND to being with, the ride would be smooth WITHOUT the fancy suspension system----
Just sayin'--------------------------
It depends on what you are trying to "fix".
Sometimes people try to fix things with the wrong tool.
Here is an analogy I like to use.
What if we made a tire that has 12 sides. Then we can use a fancy computer controlled suspension system to even out the ride. Yes it would have its drawbacks, but at least we could sell it as having "more control" (which of course it needs to begin to work properly)
WELL MAYBE----if the tire was made ROUND to being with, the ride would be smooth WITHOUT the fancy suspension system----
Just sayin'--------------------------
Re: FIR filters
In simple terms FIR crossovers have no phase shift. If needed they can have very high crossover slopes, greater than 100 dB per octave. This can have advantage for power handling and directivity issues in some cases.
The issue is often the time or latency required to implement a FIR crossover. The time required is proportional to the crossover frequency. It is a mathematical requirement and cannot be reduced by better / faster processing.
In terms of EQ - think of using an almost unlimited number of normal PEQs to create a transfer correction curve. Such a curve will only require one FIR filter / processor.
Internally FIR filters / processors are like a bunch of delay taps that feed forward and then add together. The output (EQ shape) is adjusted by modifying the delay tap coefficients.
If you consider a speaker and its enclosure as being able to be represented as a set of mathematical equations like you can with an electric circuit (we are only considering the linear behaviour) then you can mathematically adjust the input signal with an opposite equation to correct the response. Many people don’t understand this - the output is the sum of both the mechanical and electrical bits. FIR filters are very good at these types of corrections. FWIW the DIY Mid-High on this board was designed with this approach in mind. What you can’t do is fix the non-linear bits. If you try it will sound wrong and processed.
FWIW FIR filters require a lot of processing power and as such are not cheap.
In simple terms FIR crossovers have no phase shift. If needed they can have very high crossover slopes, greater than 100 dB per octave. This can have advantage for power handling and directivity issues in some cases.
The issue is often the time or latency required to implement a FIR crossover. The time required is proportional to the crossover frequency. It is a mathematical requirement and cannot be reduced by better / faster processing.
In terms of EQ - think of using an almost unlimited number of normal PEQs to create a transfer correction curve. Such a curve will only require one FIR filter / processor.
Internally FIR filters / processors are like a bunch of delay taps that feed forward and then add together. The output (EQ shape) is adjusted by modifying the delay tap coefficients.
If you consider a speaker and its enclosure as being able to be represented as a set of mathematical equations like you can with an electric circuit (we are only considering the linear behaviour) then you can mathematically adjust the input signal with an opposite equation to correct the response. Many people don’t understand this - the output is the sum of both the mechanical and electrical bits. FIR filters are very good at these types of corrections. FWIW the DIY Mid-High on this board was designed with this approach in mind. What you can’t do is fix the non-linear bits. If you try it will sound wrong and processed.
FWIW FIR filters require a lot of processing power and as such are not cheap.
Last edited:
Re: FIR filters
It's important to note that just because they can have no phase shift doesn't mean they sound good. Steep filters ring, and those 80dB/8ve+ super-steep FIR filters ring a lot... just like steep IIR filters do. But an FIR can be more than just a crossover filter.
It's important to note that just because they can have no phase shift doesn't mean they sound good. Steep filters ring, and those 80dB/8ve+ super-steep FIR filters ring a lot... just like steep IIR filters do. But an FIR can be more than just a crossover filter.
Re: FIR filters
Life, especially speaker design, involves trade-offs and compromises. Optimizing one parameter over all others will rarely end well...
Not only is there no such thing as a perfect speaker, but trying to use even ideal speakers to recreate a sound space is flawed.
FIR vs IIR is not some magic bullet for crossover filters, just another tool to be applied thoughtfully weighing the pros and cons for less cons.
JR
Life, especially speaker design, involves trade-offs and compromises. Optimizing one parameter over all others will rarely end well...
Not only is there no such thing as a perfect speaker, but trying to use even ideal speakers to recreate a sound space is flawed.
FIR vs IIR is not some magic bullet for crossover filters, just another tool to be applied thoughtfully weighing the pros and cons for less cons.
JR
Re: FIR filters
Whilst FIR filters are frequently referred to as having linear phase (or no phase variation), FIR filters can actually have almost any or arbitrary phase.
Here's a short primer which might be useful... (I hope)
A FIR filter is a filter where each output sample is just a weighted sum of a history of input samples. The filter has no feedback. For example:
s = in_sample
out_sample = 0.1 * s + 0.6 * previous_s + 0.3 * previous_previous_s
The impulse response length is just the length of the filter. Put in a 1 followed by lots of zeros and only 3 non-zero samples come output.
0.1
0.6
0.3
0
0
....
An IIR filter is similar to a FIR filter except that the sample history can feed back and sum with the input sample. For example:
s = in_sample + -0.3076 * previous_s + 0.1883 * previous_previous_s
out_sample = 0.2202 * s + 0.4404 * previous_s + 0.2202 * previous_previous_s
FWIW, this IIR is a 2nd order Butterworth at 10 kHz (at a sample rate of 48 kHz)
The impulse response length is essentially infinite, due to the feedback. Put in a 1 followed by lots of zeros, and what comes out is a series of numbers that decay toward zero and continue indefinitely:
0.22019
0.50811
0.33500
0.00733
-0.06084
-0.02009
0.00528
0.00541
0.00067
-0.00081
-0.00037
0.00004
0.00008
....
The feedback in an IIR makes for filters with steeper magnitude responses with less computation however the feedback results in some phase variation across frequency (which we're all familiar with).
For a FIR to have similar performance to an IIR, the FIR typically needs to have more coefficients and therefore requires more computation. For the IIR filter above, it takes an 11 coefficient FIR to have similar magnitude performance down to about -90 dB. It also has similar phase.
0.22019
0.50811
0.33500
0.00733
-0.06084
-0.02009
0.00528
0.00541
0.00067
-0.00081
-0.00037
So if an FIR filter is more computationally expense, why is it useful?
With enough taps (i.e. with the right length) a FIR filter can have an almost arbitrary magnitude and phase. With this flexibility, we can do things like alter the phase of a cabinet, correct for some horn internal reflection effects, and separately alter the mag/phase characteristic of each driver to improve crossover matching. This flexibility does come at the cost of delay.
Here's the same 10 kHz LPF filter (from above) but implemented as an FIR with linear phase - i.e. just bulk delay.
-0.000085851300000
-0.000259195300000
0.000070486200000
0.001712739900000
0.002552043300000
-0.006652936700000
-0.029519627600000
-0.003574233400000
0.276965408500000
0.517506320200000
0.276965408500000
-0.003574233400000
-0.029519627600000
-0.006652936700000
0.002552043300000
0.001712739900000
0.000070486200000
-0.000259195300000
-0.000085851300000
Notice the symmetry in the filter. A linear phase FIR filter has a bulk delay of half the filter length. In this case 10 samples (0.208ms). At lower frequencies, this can be 10's of milliseconds.
It's also worth noting that reversing the order of the 11 FIR taps above creates a filter with the same magnitude response, but the opposite phase or "maximum phase." In this filter, the effective delay is the full length of the filter, or 11 samples.
-0.00037
-0.00081
0.00067
0.00541
0.00528
-0.02009
-0.06084
0.00733
0.33500
0.50811
0.22019
Whilst FIR filters are frequently referred to as having linear phase (or no phase variation), FIR filters can actually have almost any or arbitrary phase.
Here's a short primer which might be useful... (I hope)
A FIR filter is a filter where each output sample is just a weighted sum of a history of input samples. The filter has no feedback. For example:
s = in_sample
out_sample = 0.1 * s + 0.6 * previous_s + 0.3 * previous_previous_s
The impulse response length is just the length of the filter. Put in a 1 followed by lots of zeros and only 3 non-zero samples come output.
0.1
0.6
0.3
0
0
....
An IIR filter is similar to a FIR filter except that the sample history can feed back and sum with the input sample. For example:
s = in_sample + -0.3076 * previous_s + 0.1883 * previous_previous_s
out_sample = 0.2202 * s + 0.4404 * previous_s + 0.2202 * previous_previous_s
FWIW, this IIR is a 2nd order Butterworth at 10 kHz (at a sample rate of 48 kHz)
The impulse response length is essentially infinite, due to the feedback. Put in a 1 followed by lots of zeros, and what comes out is a series of numbers that decay toward zero and continue indefinitely:
0.22019
0.50811
0.33500
0.00733
-0.06084
-0.02009
0.00528
0.00541
0.00067
-0.00081
-0.00037
0.00004
0.00008
....
The feedback in an IIR makes for filters with steeper magnitude responses with less computation however the feedback results in some phase variation across frequency (which we're all familiar with).
For a FIR to have similar performance to an IIR, the FIR typically needs to have more coefficients and therefore requires more computation. For the IIR filter above, it takes an 11 coefficient FIR to have similar magnitude performance down to about -90 dB. It also has similar phase.
0.22019
0.50811
0.33500
0.00733
-0.06084
-0.02009
0.00528
0.00541
0.00067
-0.00081
-0.00037
So if an FIR filter is more computationally expense, why is it useful?
With enough taps (i.e. with the right length) a FIR filter can have an almost arbitrary magnitude and phase. With this flexibility, we can do things like alter the phase of a cabinet, correct for some horn internal reflection effects, and separately alter the mag/phase characteristic of each driver to improve crossover matching. This flexibility does come at the cost of delay.
Here's the same 10 kHz LPF filter (from above) but implemented as an FIR with linear phase - i.e. just bulk delay.
-0.000085851300000
-0.000259195300000
0.000070486200000
0.001712739900000
0.002552043300000
-0.006652936700000
-0.029519627600000
-0.003574233400000
0.276965408500000
0.517506320200000
0.276965408500000
-0.003574233400000
-0.029519627600000
-0.006652936700000
0.002552043300000
0.001712739900000
0.000070486200000
-0.000259195300000
-0.000085851300000
Notice the symmetry in the filter. A linear phase FIR filter has a bulk delay of half the filter length. In this case 10 samples (0.208ms). At lower frequencies, this can be 10's of milliseconds.
It's also worth noting that reversing the order of the 11 FIR taps above creates a filter with the same magnitude response, but the opposite phase or "maximum phase." In this filter, the effective delay is the full length of the filter, or 11 samples.
-0.00037
-0.00081
0.00067
0.00541
0.00528
-0.02009
-0.06084
0.00733
0.33500
0.50811
0.22019
Re: FIR filters
Yes there will be pre and post ringing and it will be equal and opposite in the pass bands. There are ways of designing the filters to minimize this to below the point of audibility, but with everything there are some compromises.
A couple of Tims links touch on this issue. Here is another link that may be of interest.
http://www.resonessencelabs.com/digital-filters/
"The second phenomenon present in linear phase FIR filters is sometimes called “pre-ringing”. It is a tendency of the filter to output a small signal of increasing amplitude just prior to the main “step” of the signal, and then after that step has passed, ring a little at the new output level. The ringing after the step has passed is common in analog filters as well, and is due to the high Q that some filters exhibit.
Indeed this is the origin of the word “ringing”: having struck a bell with a hammer we expect it to ring a little thereafter. Pre-ringing of the symmetric FIR filter seems bizarre: it is as though the bell knows when you are going to strike it, and makes a little ringing sound before it is hit. This is very counter intuitive, and a great concern to many audiophiles, who therefore seek a filter that has no pre-ringing.
This however, cannot be achieved to perfection with linear phase filters, hence any filter designed to suppress pre-ringing completely, is dispersive. So called “Minimum Phase” filters (sometimes called “Minimum Delay” filters) are those filters that are designed to show virtually no pre-ringing (and consequently they tend to have low group delay because the maximum values in the impulse response are near the beginning of the filter). They do not have linear phase, and they consequently have dispersion.
A compromise is possible: a filter can be designed as linear phase, and hence having a symmetrical impulse response, but the coefficient list can be ‘shaped’ by what is called a ‘window’ function. This window function suppresses pre-ringing to a certain degree, but the more it suppresses pre-ringing, the more it compromises the action of the filter. That is, the more the filter fails to block the signals it is trying to stop. Such filters that apply window functions to filter coefficients in order to reduce pre-ringing are sometimes called Apodizing filters. The word means “to remove the foot”.
All the various trade-offs discussed here, but particularly Apodizing filters, show us a fundamental relationship: as a filter is designed to be optimum in the time domain, it cannot be optimum in the frequency domain. The two are related in a very fundamental way, it is the same relationship that governs the whole world of physics: Heisenberg’s Uncertainty principle that says if you know the particles position exactly, you cannot know its momentum, or vice-versa, is because mathematically one (the position for example) is the Fourier transform of the other (momentum for example) and as the “width” in position becomes better defined, the “width” in the momentum domain, being the Fourier transform, becomes less well defined."
Yes there will be pre and post ringing and it will be equal and opposite in the pass bands. There are ways of designing the filters to minimize this to below the point of audibility, but with everything there are some compromises.
A couple of Tims links touch on this issue. Here is another link that may be of interest.
http://www.resonessencelabs.com/digital-filters/
"The second phenomenon present in linear phase FIR filters is sometimes called “pre-ringing”. It is a tendency of the filter to output a small signal of increasing amplitude just prior to the main “step” of the signal, and then after that step has passed, ring a little at the new output level. The ringing after the step has passed is common in analog filters as well, and is due to the high Q that some filters exhibit.
Indeed this is the origin of the word “ringing”: having struck a bell with a hammer we expect it to ring a little thereafter. Pre-ringing of the symmetric FIR filter seems bizarre: it is as though the bell knows when you are going to strike it, and makes a little ringing sound before it is hit. This is very counter intuitive, and a great concern to many audiophiles, who therefore seek a filter that has no pre-ringing.
This however, cannot be achieved to perfection with linear phase filters, hence any filter designed to suppress pre-ringing completely, is dispersive. So called “Minimum Phase” filters (sometimes called “Minimum Delay” filters) are those filters that are designed to show virtually no pre-ringing (and consequently they tend to have low group delay because the maximum values in the impulse response are near the beginning of the filter). They do not have linear phase, and they consequently have dispersion.
A compromise is possible: a filter can be designed as linear phase, and hence having a symmetrical impulse response, but the coefficient list can be ‘shaped’ by what is called a ‘window’ function. This window function suppresses pre-ringing to a certain degree, but the more it suppresses pre-ringing, the more it compromises the action of the filter. That is, the more the filter fails to block the signals it is trying to stop. Such filters that apply window functions to filter coefficients in order to reduce pre-ringing are sometimes called Apodizing filters. The word means “to remove the foot”.
All the various trade-offs discussed here, but particularly Apodizing filters, show us a fundamental relationship: as a filter is designed to be optimum in the time domain, it cannot be optimum in the frequency domain. The two are related in a very fundamental way, it is the same relationship that governs the whole world of physics: Heisenberg’s Uncertainty principle that says if you know the particles position exactly, you cannot know its momentum, or vice-versa, is because mathematically one (the position for example) is the Fourier transform of the other (momentum for example) and as the “width” in position becomes better defined, the “width” in the momentum domain, being the Fourier transform, becomes less well defined."
Last edited:
Re: FIR filters
Haven't talked about "Gibb's phenomenon" lately..(often confused for ringing) and won't today...
y'all have google.
JR
Haven't talked about "Gibb's phenomenon" lately..(often confused for ringing) and won't today...
y'all have google.
JR
Re: FIR filters
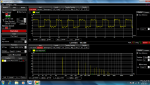
Hi JR - you asked me a while back if you could see the Gibbs phenomenon in a square wave from the DIY Mid Hi - Here is a picture that shows the Fourier Series that makes up the measured square wave which should show the Gibbs phenomenon. The resultant square wave almost does
Hi JR - you asked me a while back if you could see the Gibbs phenomenon in a square wave from the DIY Mid Hi - Here is a picture that shows the Fourier Series that makes up the measured square wave which should show the Gibbs phenomenon. The resultant square wave almost does
Attachments
Last edited:
Re: FIR filters
So if you have a speaker box with a passive crossover in it, and this passive is introducing phase shift, can you use an FIR filter to correct, or cancel this phase shift?
So if you have a speaker box with a passive crossover in it, and this passive is introducing phase shift, can you use an FIR filter to correct, or cancel this phase shift?
Re: FIR filters
Yes -- to the extent allowed by the length of the available filter and the processing delay you can tolerate. If you have the luxury of processing the signal off-line you can correct any phase anomaly perfectly. (We're talking about single-input, single output, linear, time-invariant systems and neglecting finite register length effects, bla bla bla.)
And pay attention to what Michael says.
Best,
--Frank
Yes -- to the extent allowed by the length of the available filter and the processing delay you can tolerate. If you have the luxury of processing the signal off-line you can correct any phase anomaly perfectly. (We're talking about single-input, single output, linear, time-invariant systems and neglecting finite register length effects, bla bla bla.)
And pay attention to what Michael says.
Best,
--Frank
Re: FIR filters
For the last 16 months I've been working on a PC/Mac application to design arbitrary FIR filters for DSP based loudspeakers and install systems with FIR DSP capability. This project was prompted by a conversation with Bennett at CEDIA in 2014 about using FIR to correct phase.
I've put some screenshots at the link below for anyone who's interested.
https://www.facebook.com/media/set/...073741826.537879272890039&type=1&l=b2f972b074
Some of you have been helping with Alpha/Beta testing already. You know who you are. Thank you very much! I hope to have this ready for proper release in the next few months.
Cheers,
For the last 16 months I've been working on a PC/Mac application to design arbitrary FIR filters for DSP based loudspeakers and install systems with FIR DSP capability. This project was prompted by a conversation with Bennett at CEDIA in 2014 about using FIR to correct phase.
I've put some screenshots at the link below for anyone who's interested.
https://www.facebook.com/media/set/...073741826.537879272890039&type=1&l=b2f972b074
Some of you have been helping with Alpha/Beta testing already. You know who you are. Thank you very much! I hope to have this ready for proper release in the next few months.
Cheers,
Re: FIR filters
Michael … great work …fantastic stuff, can’t wait to see what you have come up with~~:smile: …
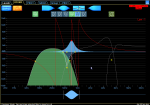
This topic is all about how FIR filters work, not my DIY project, but this is exactly what I have done with the Lake processing – I used both FIR and IIR filters, but also separately flattened the phase response as much as I was prepared to tolerate in terms of increasing the system latency so that I had a flat phase response across the critical vocal region. Refer the red phase correction trace.
Quit a few people are starting to do this; Dave Gunness does this with Fulcrum speakers and previously for EAW’s with their (Gunness) focusing.
Four audio are also doing this with their processor and Monkey Forrest software. http://www.fouraudio.com/en/home.html
http://www.four-audio.com/data/AES32/AES32FourAudio.pdf
It’s also possible with this FIR engine http://aplaudio.com/conc2/products/apl1s/ and the associated software, but I don’t think the phase correction is enabled at this stage.
Jack, I have done exactly what you asked with the passive crossover for your BMS4594 using a Lake LM26.
Michael … great work …fantastic stuff, can’t wait to see what you have come up with
~~:smile: …This topic is all about how FIR filters work, not my DIY project, but this is exactly what I have done with the Lake processing – I used both FIR and IIR filters, but also separately flattened the phase response as much as I was prepared to tolerate in terms of increasing the system latency so that I had a flat phase response across the critical vocal region. Refer the red phase correction trace.
Quit a few people are starting to do this; Dave Gunness does this with Fulcrum speakers and previously for EAW’s with their (Gunness) focusing.
Four audio are also doing this with their processor and Monkey Forrest software. http://www.fouraudio.com/en/home.html
http://www.four-audio.com/data/AES32/AES32FourAudio.pdf
It’s also possible with this FIR engine http://aplaudio.com/conc2/products/apl1s/ and the associated software, but I don’t think the phase correction is enabled at this stage.
Jack, I have done exactly what you asked with the passive crossover for your BMS4594 using a Lake LM26.
Attachments
Re: FIR filters
I wont admit to knowing/understanding everything that Dave is doing even after reading his papers/patents many many times (maybe he will drop by here again), however I do know that his use of FIR filters goes far beyond that of simply flattening the phase response of a system.
15 posts in and no one has mentioned Rephase yet. If all you are looking to do is adjust the magnitude and phase response independently then play around a little with Rephase. I have had good luck importing Smaart transfer functions, creating my adjustments, and having it spit out a FIR coefficients.
I wont admit to knowing/understanding everything that Dave is doing even after reading his papers/patents many many times (maybe he will drop by here again), however I do know that his use of FIR filters goes far beyond that of simply flattening the phase response of a system.
15 posts in and no one has mentioned Rephase yet. If all you are looking to do is adjust the magnitude and phase response independently then play around a little with Rephase. I have had good luck importing Smaart transfer functions, creating my adjustments, and having it spit out a FIR coefficients.
Re: FIR filters
I understand it about as much as I understand how my car works. I get the basic idea of a combustion engine, fuel/air mix, and the mechanics that move the wheels... but if I needed to actually build it myself it wouldn't work.
Here's the Fulcrum page on TEQ: http://www.fulcrum-acoustic.com/technologies/temporal-eq.html Some of Dave's white papers have graphs that make it more clear what is being corrected in the time domain, shown using wavelet responses. It does take a lot of processing, but the final result is achieved without significant latency. IIRC about 1.4msec, most of which is due to the A/D D/A conversion.
Fulcrum aren't the only ones doing interesting stuff with FIRs commercially, but they do go into the most detail about what they're doing so it's a great resource.
I understand it about as much as I understand how my car works. I get the basic idea of a combustion engine, fuel/air mix, and the mechanics that move the wheels... but if I needed to actually build it myself it wouldn't work.
Here's the Fulcrum page on TEQ: http://www.fulcrum-acoustic.com/technologies/temporal-eq.html Some of Dave's white papers have graphs that make it more clear what is being corrected in the time domain, shown using wavelet responses. It does take a lot of processing, but the final result is achieved without significant latency. IIRC about 1.4msec, most of which is due to the A/D D/A conversion.
Fulcrum aren't the only ones doing interesting stuff with FIRs commercially, but they do go into the most detail about what they're doing so it's a great resource.
Re: FIR filters
Just to add a "different twist" to the whole eq/phase issue.
Just because an eq adjust the phase DOES NOT always mean it is a bad thing.
If it is in a "problem area" then it could possibly help to have an eq that does not adjust phase.
HOWEVER-in many cases (where there is no overlap-multi arrivals etc) when you adjust the eq you ACTUALLY HELP the phase response to be flatter.
So "automatically" assuming that FIR is the "ultimate answer" is going down the wrong road.
As usual-it depends, and when a proper speaker design is done, you do NOT need FIR filters. Because there is nothing to "fix".
Or put another way-often "fancy filters" (of all types) are trying to fix something that is basically a bad/incorrect design.
If it was a better design, then you don't need the "fancy filters".
A "perfect speaker" will have a phase response that resembles a high and low pass filter.
Once you get past that-you are dealing with compromised designs. Some need more help than others.
And something that is often overlooked, is while the "fancy filters" may appear to fix the issues in one listening position, WHAT ABOUT ALL THE OTHERS????? In many cases they get worse.
But I guess as long as the measurement position is happy-then all is well.
But in many cases the GOAL should be to provide THE SAME response to all listeners.
Just to add a "different twist" to the whole eq/phase issue.
Just because an eq adjust the phase DOES NOT always mean it is a bad thing.
If it is in a "problem area" then it could possibly help to have an eq that does not adjust phase.
HOWEVER-in many cases (where there is no overlap-multi arrivals etc) when you adjust the eq you ACTUALLY HELP the phase response to be flatter.
So "automatically" assuming that FIR is the "ultimate answer" is going down the wrong road.
As usual-it depends, and when a proper speaker design is done, you do NOT need FIR filters. Because there is nothing to "fix".
Or put another way-often "fancy filters" (of all types) are trying to fix something that is basically a bad/incorrect design.
If it was a better design, then you don't need the "fancy filters".
A "perfect speaker" will have a phase response that resembles a high and low pass filter.
Once you get past that-you are dealing with compromised designs. Some need more help than others.
And something that is often overlooked, is while the "fancy filters" may appear to fix the issues in one listening position, WHAT ABOUT ALL THE OTHERS????? In many cases they get worse.
But I guess as long as the measurement position is happy-then all is well.
But in many cases the GOAL should be to provide THE SAME response to all listeners.
Re: FIR filters
I use this thought all the time in determining whether a change in eq should be made based on a measurement. The proposed change should improve things in both remain.
Sent from my XT1254
I use this thought all the time in determining whether a change in eq should be made based on a measurement. The proposed change should improve things in both remain.
Sent from my XT1254
Re: FIR filters
I agree. Non-flat phase isn't inherently a bad thing.
Part of my motivation for creating a FIR tool was to have the ability to easily match speakers of different makes/models in a system; mains, delays etc. - flat phase or otherwise. Speaker matching using minimum phase filtering and delay, in typical speaker processors, is not impossible but it can be difficult and/or time consuming.
I agree. Non-flat phase isn't inherently a bad thing.
Part of my motivation for creating a FIR tool was to have the ability to easily match speakers of different makes/models in a system; mains, delays etc. - flat phase or otherwise. Speaker matching using minimum phase filtering and delay, in typical speaker processors, is not impossible but it can be difficult and/or time consuming.