I've been working on just this problem. Synthesizing arbitrary FIR filters given a prototype response is comparatively easy, although there, too, are some tricks that they didn't teach us in school, as we discussed in Montreal.
At this point my approach to obtaining a prototype response is to generate a minimum phase FIR filter from the smoothed, statistically combined log-magnitude of multiple measurements. This takes out pretty much all of the fine detail ("grass") in the magnitude and phase response and, since the filter depends on magnitude alone, the time alignment of the individual measurements is irrelevant. Furthermore, the relative gains of the individual measurements also are irrelevant as the log-magnitudes, rather than the magnitudes, are being averaged.
I combine (convolve) this filter with an FIR all-pass to take out the excess phase. The beauty is that excess phase anomalies tend to vary slowly with frequency and angle (except in the top octave of certain compression drivers, it seems) so the time alignment of the measurements is not that critical. Simply aligning the peaks of the impulse responses (to the nearest sample) appears to be sufficient. The absolute time alignment is also irrelevant, as I normalize the combined group delay so that the filter is "doing as little as possible". We don't care about bulk delay of the entire signal, within reason. Normalizing the derivative of the phase (group delay) is analogous to normalizing the the log-magnitude in the minimum phase filter.
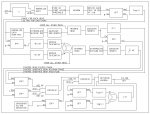
In due course I'll post some signal flow charts (block diagrams) and typical graphs here. It'll take me a bit to get it all together. I'm likely reinventing the wheel (and maybe getting it wrong) but I'm having fun.
Best,
--Frank